https://www.quantamagazine.org/how-the- ... -20240903/
Ymmärrettävä fysikaalisuuteen pohjautuva sopivasti popularisoiva selostus.
Koetan tiivistää Higgsin yhteen viestiin samalla, kun kertaan asian itselleni. Jätän pois paljon laskuja, yksityiskohtia ja selityksiä. Vain periaatteet mukana.
Vapaan massallisen Diracin kentän (spin-½) Lagrangen tiheys on
\(\mathcal{L}_{D}=\bar\Psi(i\gamma_\mu\partial^\mu-m)\Psi\)
missä \(\Psi\) on Diracin spinori, \(m\) on massa, \(\gamma_\mu\) ovat Diracin matriisit, ja \(\bar\Psi=\Psi^\dagger\gamma_0\). Tämä \(\mathcal{L}_{D}\) on invariantti Lorentz-muunnoksissa, se siis toteuttaa \(SO(1,3)\)-symmetrian.
Lokaali \(U(1)\)-symmetria tarkoittaa sitä, että Lagrangen tiheys on invariantti muunnoksessa
\(\begin{align*}
\Psi &\to e^{ia(x)}\Psi\\
\bar\Psi &\to \bar\Psi e^{-ia(x)}
\end{align*}\)
missä \(a(x) \in \mathbb{R}\) on paikasta \(x^\mu=(x^0,x^1,x^2,x^3)\) riippuva funktio. Vapaan kentän \(\mathcal{L}_{D}\) ei ole invariantti lokaalissa \(U(1)\)-muunnoksessa. Se on tosin invariantti globaalissa \(U(1)\)-muunnoksessa \(\Psi \to e^{ia}\Psi\), missä \(a \in \mathbb{R}\) on vakio.
Vapaan ja massattoman fotonikentän (spin-1) Lagrangen tiheys
\(\mathcal{L}_{EM}=\partial^\mu A^\nu\partial_\mu A_\nu - \partial^\mu A^\nu\partial_\nu A_\mu\)
ei ole invariantti lokaalissa muunnoksessa \(A_\mu\to A_\mu+a_\mu(x)\), mutta on invariantti lokaalissa muunnoksessa \(A_\mu\to A_\mu+\partial_\mu a(x)\), missä mukana funktion \(a(x)\) derivaatta.
\(\mathcal{L}_{D}\) ja \(\mathcal{L}_{EM}\) voidaan kuitenkin yhdistää siten, että se toteuttaa lokaalin \(U(1)\)-symmetrian
\(\begin{align*}
\mathcal{L}_{QED}&=-m\bar\Psi\Psi+i\bar\Psi\gamma_\mu(\partial^\mu-igA^\mu)\Psi-\frac{1}{4}(\partial^\mu A^\nu\partial_\mu A_\nu - \partial^\mu A^\nu\partial_\nu A_\mu)\\
&=-m\bar\Psi\Psi+i\bar\Psi\gamma_\mu D^\mu \Psi-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}
\end{align*}\)
missä \(g\) on kytkinvakio (varaus). Toisella rivillä \(D^\mu=i\partial^\mu-ig A^\mu\) on kovariantti derivaatta, ja \(F_{\mu\nu}\) on sähkömagneettinen kenttävoimakkuustensori. \(A_\mu\) saa nimen \(U(1)\)-mittakenttä, sillä se mahdollistaa lokaalin \(U(1)\)-symmetrian, ja kenttien vuorovaikutuksen.
Vapaa Diracin kenttä voidaan kirjoittaa myös massattomana
\(\mathcal{L}_{F}=i\bar\Psi\gamma_\mu\partial^\mu\Psi\)
missä \(\Psi\) ja \(\bar\Psi\) sisältävät kaksi komponenttia
\(\begin{align*}
\Psi&=\begin{pmatrix} \psi_1\\ \psi_2\end{pmatrix}\\
\bar\Psi&=\begin{pmatrix} \bar\psi_1 & \bar\psi_2\end{pmatrix}
\end{align*}\)
Kenttiä \(\Psi\) ja \(\bar\Psi\) kutsutaan nimellä dupletti. Massaton \(\mathcal{L}_{F}\) toteuttaa globaalin \(SU(2)\)-symmetrian, jonka muunnokset ovat
\(\begin{align*}
\Psi &\to e^{ia_i\frac{\sigma_i}{2}} \Psi\\
\bar\Psi &\to \bar\Psi e^{-ia_i\frac{\sigma_i}{2}}
\end{align*}\)
Tässä \(\sigma_i\) ovat 3 Paulin matriisia, ja \(a_i\) vakiot näiden edessä. Eksponentissa on summattuna 3 Paulin matriisia kertoimineen.
Paulin matriisit ovat ryhmän \(SU(2)\) generaattoreita. Lokaalin \(SU(2)\)-muunnoksen kerroin on \(e^{ia_i(x)\frac{\sigma_i}{2}} \in SU(2)\). Massaton \(\mathcal{L}_{F}\) ei toteuta lokaalia \(SU(2)\)-symmetriaa. Osoittautuu, että lokaalin symmetrian toteuttava Lagrange on
\(\mathcal{L}_{F+B}=i\bar\Psi\gamma_\mu D^\mu\Psi - \frac{1}{4}Tr(B_{\mu\nu}B^{\mu\nu})\)
missä massaton spin-½ ja \(B^\mu\) -kenttä vuorovaikuttavat. Lagrangen tiheydessä on kenttävoimakkuustensori
\(B^{\mu\nu}=\partial^\mu B^\nu - \partial^\nu B^\mu - i g_w [B^\mu,B^\nu]\)
Tässä \(B^\mu\) on matriisi, ja viimeinen termi on matriisikommutointi. Kytkinvakio on \(g_w\).
Matriisi \(B^\mu = (W^\mu)_i\frac{\sigma^i}{2}\), missä komponentit \(\mu=\{0,1,2,3\}\). Indekseistä \(i=\{1,2,3\}\) muodostuu kolmen Paulin matriisin summa.
\(B^\mu\) sisältää näin kolme spin-1 kenttää \((W^\mu)_i\), jotka ovat \(SU(2)\)-mittakenttiä. Kovariantti derivaatta on \(D^\mu =\partial^\mu-i g_w B^\mu\). Nyt voidaan yhdistää lokaalit symmetriat \(U(1)\) ja \(SU(2)\) kirjoittamalla
\(\mathcal{L}_{F+B+EM}=i\bar\Psi\gamma_\mu (\partial^\mu-igA^\mu-i g_w B^\mu)\Psi - \frac{1}{4}Tr(B_{\mu\nu}B^{\mu\nu})-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}\)
missä \(g\) on \(U(1)\)-mittakentän kytkinvakio, ja \(g_w\) on \(SU(2)\)-mittakentän kytkinvakio. Tästä kuitenkin puuttuu fermioni-kentän massa \(m\) (tarkemmin dupletin massat \(m_1\) ja \(m_2\)), joka rikkoisi \(U(1)\)- ja \(SU(2)\)-symmetriat.
Seuraavaksi kirjoitetaan skalaarikenttä (spin-0)
\(\mathcal{L}_H = \partial_\mu\phi^\dagger\partial^\mu\phi-\rho^2\phi^\dagger\phi-\lambda(\phi^\dagger\phi)^2\)
missä \(\phi\) on kompleksinen, ja \(\rho\) on massaparametri. \(\lambda\) ilmaisee itsevuorovaikutuksen voimakkuuden. Kyseessä ei siis ole täysin vapaa kenttä. Yhdistetään massaton fotonikenttä ja skalaarikenttä
\(\mathcal{L}_{EM+H} = ((\partial_\mu+igA_\mu)\phi^\dagger)((\partial^\mu-igA^\mu)\phi)+\rho^2\phi^\dagger\phi-\lambda(\phi^\dagger\phi)^2\)
mikä toteuttaa lokaalin \(U(1)\)-symmetrian. Sitten kirjoitetaan skalaarikenttä duplettina
\(\Phi=\begin{pmatrix} \phi_1\\ \phi_2 \end{pmatrix}\)
Tämän jälkeen fotoni-, skalaari- ja \(B^\mu\)-kenttä yhdistetään
\(\mathcal{L}_{EM+B+H}=((\partial_\mu+ig_wB^\mu+igA_\mu)\Phi^\dagger)((\partial^\mu-ig_wB^\mu-igA^\mu)\Phi)+\rho^2\Phi^\dagger\Phi-\lambda(\Phi^\dagger\Phi)^2\)
Myös tämä \(\mathcal{L}_{EM+B+H}\) toteuttaa lokaalin \(SU(2)\)-symmetrian. Poimitaan vielä potentiaali
\(\begin{align*}
V(\Phi)&=\rho^2\Phi^\dagger\Phi-\lambda(\Phi^\dagger\Phi)^2 \\
&=-\rho^2\phi_1^\dagger\phi_1+\lambda(\phi_1^\dagger\phi_1)^2-\rho^2\phi_2^\dagger\phi_2+\lambda(\phi_2^\dagger\phi_2)^2 \\
&=V(\phi_1)+V(\phi_2)
\end{align*}\)
Dupletin komponenteille voidaan laskea arvo, joka minimoi potentiaalin. Tämä arvo on \(\phi_m =\sqrt{\frac{\rho^2}{2\lambda}}\ e^{i\varphi}\), missä \(e^{i\varphi}\) on vaihekerroin. Potentiaalia \(V(\Phi)=V(\phi_1)+V(\phi_2)\) kutsutaan nimellä Higgsin potentiaali ja sen minimiarvo vastaa kentän perustilaa.
Yksi viesti riitti hädin tuskin puoleen väliin. Kirjoitan joskus toisen viestin. Joskus
Vapaan massallisen Diracin kentän (spin-½) Lagrangen tiheys on
\(\mathcal{L}_{D}=\bar\Psi(i\gamma_\mu\partial^\mu-m)\Psi\)
missä \(\Psi\) on Diracin spinori, \(m\) on massa, \(\gamma_\mu\) ovat Diracin matriisit, ja \(\bar\Psi=\Psi^\dagger\gamma_0\). Tämä \(\mathcal{L}_{D}\) on invariantti Lorentz-muunnoksissa, se siis toteuttaa \(SO(1,3)\)-symmetrian.
Lokaali \(U(1)\)-symmetria tarkoittaa sitä, että Lagrangen tiheys on invariantti muunnoksessa
\(\begin{align*}
\Psi &\to e^{ia(x)}\Psi\\
\bar\Psi &\to \bar\Psi e^{-ia(x)}
\end{align*}\)
missä \(a(x) \in \mathbb{R}\) on paikasta \(x^\mu=(x^0,x^1,x^2,x^3)\) riippuva funktio. Vapaan kentän \(\mathcal{L}_{D}\) ei ole invariantti lokaalissa \(U(1)\)-muunnoksessa. Se on tosin invariantti globaalissa \(U(1)\)-muunnoksessa \(\Psi \to e^{ia}\Psi\), missä \(a \in \mathbb{R}\) on vakio.
Vapaan ja massattoman fotonikentän (spin-1) Lagrangen tiheys
\(\mathcal{L}_{EM}=\partial^\mu A^\nu\partial_\mu A_\nu - \partial^\mu A^\nu\partial_\nu A_\mu\)
ei ole invariantti lokaalissa muunnoksessa \(A_\mu\to A_\mu+a_\mu(x)\), mutta on invariantti lokaalissa muunnoksessa \(A_\mu\to A_\mu+\partial_\mu a(x)\), missä mukana funktion \(a(x)\) derivaatta.
\(\mathcal{L}_{D}\) ja \(\mathcal{L}_{EM}\) voidaan kuitenkin yhdistää siten, että se toteuttaa lokaalin \(U(1)\)-symmetrian
\(\begin{align*}
\mathcal{L}_{QED}&=-m\bar\Psi\Psi+i\bar\Psi\gamma_\mu(\partial^\mu-igA^\mu)\Psi-\frac{1}{4}(\partial^\mu A^\nu\partial_\mu A_\nu - \partial^\mu A^\nu\partial_\nu A_\mu)\\
&=-m\bar\Psi\Psi+i\bar\Psi\gamma_\mu D^\mu \Psi-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}
\end{align*}\)
missä \(g\) on kytkinvakio (varaus). Toisella rivillä \(D^\mu=i\partial^\mu-ig A^\mu\) on kovariantti derivaatta, ja \(F_{\mu\nu}\) on sähkömagneettinen kenttävoimakkuustensori. \(A_\mu\) saa nimen \(U(1)\)-mittakenttä, sillä se mahdollistaa lokaalin \(U(1)\)-symmetrian, ja kenttien vuorovaikutuksen.
Vapaa Diracin kenttä voidaan kirjoittaa myös massattomana
\(\mathcal{L}_{F}=i\bar\Psi\gamma_\mu\partial^\mu\Psi\)
missä \(\Psi\) ja \(\bar\Psi\) sisältävät kaksi komponenttia
\(\begin{align*}
\Psi&=\begin{pmatrix} \psi_1\\ \psi_2\end{pmatrix}\\
\bar\Psi&=\begin{pmatrix} \bar\psi_1 & \bar\psi_2\end{pmatrix}
\end{align*}\)
Kenttiä \(\Psi\) ja \(\bar\Psi\) kutsutaan nimellä dupletti. Massaton \(\mathcal{L}_{F}\) toteuttaa globaalin \(SU(2)\)-symmetrian, jonka muunnokset ovat
\(\begin{align*}
\Psi &\to e^{ia_i\frac{\sigma_i}{2}} \Psi\\
\bar\Psi &\to \bar\Psi e^{-ia_i\frac{\sigma_i}{2}}
\end{align*}\)
Tässä \(\sigma_i\) ovat 3 Paulin matriisia, ja \(a_i\) vakiot näiden edessä. Eksponentissa on summattuna 3 Paulin matriisia kertoimineen.
Paulin matriisit ovat ryhmän \(SU(2)\) generaattoreita. Lokaalin \(SU(2)\)-muunnoksen kerroin on \(e^{ia_i(x)\frac{\sigma_i}{2}} \in SU(2)\). Massaton \(\mathcal{L}_{F}\) ei toteuta lokaalia \(SU(2)\)-symmetriaa. Osoittautuu, että lokaalin symmetrian toteuttava Lagrange on
\(\mathcal{L}_{F+B}=i\bar\Psi\gamma_\mu D^\mu\Psi - \frac{1}{4}Tr(B_{\mu\nu}B^{\mu\nu})\)
missä massaton spin-½ ja \(B^\mu\) -kenttä vuorovaikuttavat. Lagrangen tiheydessä on kenttävoimakkuustensori
\(B^{\mu\nu}=\partial^\mu B^\nu - \partial^\nu B^\mu - i g_w [B^\mu,B^\nu]\)
Tässä \(B^\mu\) on matriisi, ja viimeinen termi on matriisikommutointi. Kytkinvakio on \(g_w\).
Matriisi \(B^\mu = (W^\mu)_i\frac{\sigma^i}{2}\), missä komponentit \(\mu=\{0,1,2,3\}\). Indekseistä \(i=\{1,2,3\}\) muodostuu kolmen Paulin matriisin summa.
\(B^\mu\) sisältää näin kolme spin-1 kenttää \((W^\mu)_i\), jotka ovat \(SU(2)\)-mittakenttiä. Kovariantti derivaatta on \(D^\mu =\partial^\mu-i g_w B^\mu\). Nyt voidaan yhdistää lokaalit symmetriat \(U(1)\) ja \(SU(2)\) kirjoittamalla
\(\mathcal{L}_{F+B+EM}=i\bar\Psi\gamma_\mu (\partial^\mu-igA^\mu-i g_w B^\mu)\Psi - \frac{1}{4}Tr(B_{\mu\nu}B^{\mu\nu})-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}\)
missä \(g\) on \(U(1)\)-mittakentän kytkinvakio, ja \(g_w\) on \(SU(2)\)-mittakentän kytkinvakio. Tästä kuitenkin puuttuu fermioni-kentän massa \(m\) (tarkemmin dupletin massat \(m_1\) ja \(m_2\)), joka rikkoisi \(U(1)\)- ja \(SU(2)\)-symmetriat.
Seuraavaksi kirjoitetaan skalaarikenttä (spin-0)
\(\mathcal{L}_H = \partial_\mu\phi^\dagger\partial^\mu\phi-\rho^2\phi^\dagger\phi-\lambda(\phi^\dagger\phi)^2\)
missä \(\phi\) on kompleksinen, ja \(\rho\) on massaparametri. \(\lambda\) ilmaisee itsevuorovaikutuksen voimakkuuden. Kyseessä ei siis ole täysin vapaa kenttä. Yhdistetään massaton fotonikenttä ja skalaarikenttä
\(\mathcal{L}_{EM+H} = ((\partial_\mu+igA_\mu)\phi^\dagger)((\partial^\mu-igA^\mu)\phi)+\rho^2\phi^\dagger\phi-\lambda(\phi^\dagger\phi)^2\)
mikä toteuttaa lokaalin \(U(1)\)-symmetrian. Sitten kirjoitetaan skalaarikenttä duplettina
\(\Phi=\begin{pmatrix} \phi_1\\ \phi_2 \end{pmatrix}\)
Tämän jälkeen fotoni-, skalaari- ja \(B^\mu\)-kenttä yhdistetään
\(\mathcal{L}_{EM+B+H}=((\partial_\mu+ig_wB^\mu+igA_\mu)\Phi^\dagger)((\partial^\mu-ig_wB^\mu-igA^\mu)\Phi)+\rho^2\Phi^\dagger\Phi-\lambda(\Phi^\dagger\Phi)^2\)
Myös tämä \(\mathcal{L}_{EM+B+H}\) toteuttaa lokaalin \(SU(2)\)-symmetrian. Poimitaan vielä potentiaali
\(\begin{align*}
V(\Phi)&=\rho^2\Phi^\dagger\Phi-\lambda(\Phi^\dagger\Phi)^2 \\
&=-\rho^2\phi_1^\dagger\phi_1+\lambda(\phi_1^\dagger\phi_1)^2-\rho^2\phi_2^\dagger\phi_2+\lambda(\phi_2^\dagger\phi_2)^2 \\
&=V(\phi_1)+V(\phi_2)
\end{align*}\)
Dupletin komponenteille voidaan laskea arvo, joka minimoi potentiaalin. Tämä arvo on \(\phi_m =\sqrt{\frac{\rho^2}{2\lambda}}\ e^{i\varphi}\), missä \(e^{i\varphi}\) on vaihekerroin. Potentiaalia \(V(\Phi)=V(\phi_1)+V(\phi_2)\) kutsutaan nimellä Higgsin potentiaali ja sen minimiarvo vastaa kentän perustilaa.
Yksi viesti riitti hädin tuskin puoleen väliin. Kirjoitan joskus toisen viestin. Joskus
SI Resurrection!
Lisätään vielä se, että on äärimmäisen antoisaa rakentaa siltoja puhtaan matematiikan esitysten ja fysiikan esitysten välillä. Hyvin monesti on hankalaa ymmärtää sen toisen osapuolen argumentteja.
Valtaosa materiaalista valitsee puolensa ja siten on monesti hankalaa löytää sellaisia juttuja, jotka olisivat tyydyttäviä kummallekkin, paremminkin kumpikin kokee sen toisen esityksen jotenkin epäselväksi, vaaativaksi tms. Tämä siis koskee jotain graduate-tason juttuja.
Valtaosa materiaalista valitsee puolensa ja siten on monesti hankalaa löytää sellaisia juttuja, jotka olisivat tyydyttäviä kummallekkin, paremminkin kumpikin kokee sen toisen esityksen jotenkin epäselväksi, vaaativaksi tms. Tämä siis koskee jotain graduate-tason juttuja.
SI Resurrection!
Fyysikot eivät usein itsekään ymmärrä valintojaan matematiikan näkökulmasta. Myöhempinä vuosina tyypillisesti joku matemaatikko selittää mitä ovat oikeasti touhunneet 
Aiheena oleva sähköheikko teoria ja Higgs sisältää sekin sekavan seurakunnan verran fysiikkaan perustuvia valintoja ja selittelyjä. Voisin ekaa viestiäni joskus purkaa osiin pala kerrallaan. Sitä ennen kirjoitan lisäviestin, jossa koetan selittää periaatteellisesti sen, miten Higgs antaa fermionille massan.
Hiukkasfysiikan standardimalli on ruma teoria, jota ei kai voi kaikilta osin saada matemaattisesti kauniiksi. Mutta esim lokaali SU(2)-symmetria näyttää siltä, että on ehkä olemassa elegantti geometrinen tapa. Viittasitkin konnektioihin ja kimppuihin, joita tähän liittyy.
SU(2)-mittakentän muodostus brute force päättelyllä on sotkuinen. Geometrinen menetelmä olisi ehkä jopa yksinkertaisempi. Pitää etsiä lähteitä aiheesta.
Aiheena oleva sähköheikko teoria ja Higgs sisältää sekin sekavan seurakunnan verran fysiikkaan perustuvia valintoja ja selittelyjä. Voisin ekaa viestiäni joskus purkaa osiin pala kerrallaan. Sitä ennen kirjoitan lisäviestin, jossa koetan selittää periaatteellisesti sen, miten Higgs antaa fermionille massan.
Hiukkasfysiikan standardimalli on ruma teoria, jota ei kai voi kaikilta osin saada matemaattisesti kauniiksi. Mutta esim lokaali SU(2)-symmetria näyttää siltä, että on ehkä olemassa elegantti geometrinen tapa. Viittasitkin konnektioihin ja kimppuihin, joita tähän liittyy.
SU(2)-mittakentän muodostus brute force päättelyllä on sotkuinen. Geometrinen menetelmä olisi ehkä jopa yksinkertaisempi. Pitää etsiä lähteitä aiheesta.
Mulla oli etumerkkivirhe potentiaalissa. Korjasin
\(\begin{align*}
\mathcal{L}_{EM+B+H}&=((\partial_\mu+ig_wB_\mu+igA_\mu)\Phi^\dagger)((\partial^\mu-ig_wB^\mu-igA^\mu)\Phi)+\rho^2\Phi^\dagger\Phi-\lambda(\Phi^\dagger\Phi)^2 \\
&=((\partial_\mu+ig_w[\ (W_\mu)_i\frac{\sigma_i}{2} \ ]+igA_\mu)\Phi^\dagger)((\partial^\mu-ig_w[\ (W^\mu)_i\frac{\sigma_i}{2} \ ]-igA^\mu)\Phi)-V(\Phi^\dagger\Phi)
\end{align*}\)
missä yhdistetty mittakentät \(A^\mu\) ja \(B^\mu\) sekä kompleksinen skalaarikenttä \(\Phi\) (Higgsin dupletti). Toisella rivillä potentiaali \(V(\Phi^\dagger\Phi)\), ja \(SU(2)\)-mittakenttä komponenteilla \(W_1\), \(W_2\) ja \(W_3\).
Kuvassa pystyakseli on \(V\) ja vaaka-akseli \(\Phi\).
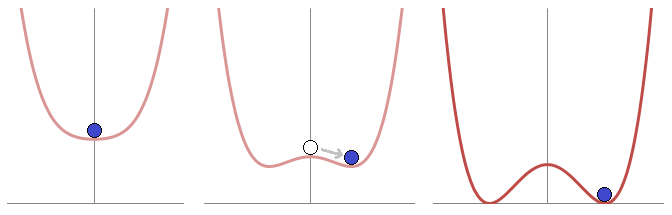
Vasemmalla \(V\) minimoituu, kun \(\Phi=0\), ja parametrit \(\rho=0\), \(\lambda>0\).
Keskellä \(\rho>0\) ja \(\lambda>0\). Minimi on kahdessa eri paikassa.
Higgsin potenatiaali on likimain kuten oikeanpuoleinen kuva. Minimi \(V=0\) on kahdessa eri paikassa, joissa kentän arvo \(\Phi \neq 0\).
Minimi saavutetaan siis kohdissa, joissa kentän arvo on nollasta poikkeava. Vaaka-akselin pitäisi tosin olla taso \((\ Re(\Phi), Im(\Phi)\ )\), missä \(V(\Phi)=0\) muodostaa kuuluisan meksikolaisen hatun alimman kohdan. Potentiaalin minimoi kenttä, jolle kaikissa avaruuden pisteissä \(x\) pätee \(\Phi^\dagger\Phi=\frac{\rho^2}{2\lambda}\).
Usein sanotaan, että \(U(1) \times SU(2)\)-symmetria rikkoutuu spontaanisti, kun \(V(\Phi)\):n konfiguraatio siirtyy vasemman kuvan tilanteesta kohti oikeaa. Ennen symmetriarikkoa Diracin kenttä on massaton ja sen Lagrange lokaalisti \(SU(2)\)-symmetrinen.
Skalaari-dupletin \(\Phi\) komponenteilla \(\phi_1\) ja \(\phi_2\) on potentiaalit \(V(\phi_1^\dagger\phi_1)\) ja \(V(\phi_2^\dagger\phi_2)\) sekä näiden minimit. Minimejä vastaavat arvot ovat \(\phi_{1min}\) ja \(\phi_{2min}\). On ääretön määrä minimin tuottavia kentän arvoja, jotka ovat origoa kiertävällä ympyrällä. Arvoista poimitaan mittavalinta. Hyväksi valinnaksi osoittautuu (perustelut sikseen)
\(\Phi_{min}=\begin{pmatrix} \phi_{1min}\\\phi_{2min} \end{pmatrix} = \frac{1}{\sqrt{2}}\begin{pmatrix} 0\\ v+\eta \end{pmatrix}\)
missä \(v = \pm \sqrt{\frac{\rho^2}{\lambda}}\) on vakio, ja \(\eta\) on kenttä, joka korvaa komponentit \(\phi_1\) ja \(\phi_2\). Valinnan nimitys on unitaarimitta. Dupletin \(\Phi\) neljästä arvosta (2 reaalista, 2 kompleksista) jäljellä on yksi reaalinen \(\eta\), jonka nimi on Higgsin kenttä. Loput 3 ovat poistuneet mittavalinnan seurauksena, ja lisäksi \(V(\Phi^\dagger\Phi)\) minimoituu Higgsin kentän arvolla \(\eta=0\).
Lagrangen tiheyteen \(\mathcal{L}_{EM+B+H}\) sijoitetaan Higgsin potentiaalin minimiä \(V(\Phi^\dagger\Phi)=0\) vastaava Higgsin dupletti \(\Phi_{min}\) siten, että käytetään unitaarimittaa
\(\mathcal{L}_{EM+B+H}^{\text{unitary}} = \frac{v^2}{8}\left[g_w^2 (W_1^\mu)^2+g_w^2 (W_2^\mu)^2+ (g_w W^\mu_3-gA^\mu)^2\right]\)
Määritellään \(SU(2)\)-mittakenttä hiukan toisin
\(\begin{align*}
W_+^\mu&=\frac{1}{\sqrt{2}}(W_1^\mu-iW_2^\mu)\\
W_-^\mu&=\frac{1}{\sqrt{2}}(W_1^\mu+iW_2^\mu)
\end{align*}\)
jolloin
\(\mathcal{L}_{EM+B+H}^{\text{unitary}} = \frac{1}{4}v^2 g_w^2 (W_+)_\mu(W_-)^\mu + \frac{1}{8}v^2(g_w W^\mu_3-gA^\mu)^2\)
Jälkimmäinen termi voidaan kirjoittaa matriisimuodossa
\((g_w W^\mu_3-gA^\mu)^2 = (W_3^\mu,A_\mu)
\begin{bmatrix}
g_w^2 & -gg_w \\
-gg_w & g^2
\end{bmatrix}
\begin{pmatrix} W_3^\mu \\ A_\mu \end{pmatrix}\)
missä matriisin molemmin puolin vektori \((W_3^\mu,A_\mu)\). Matriisi diagonalisoidaan, ja \(W_3^\mu\) nimetään erinäisiä kertoimia käyttäen \(Z^\mu\) (perustelu jääköön sikseen tässä kohti). Näin saadaan
\(\mathcal{L}_{EM+B+H}^{\text{unitary}} = \frac{1}{4}v^2 g_w^2 (W_+)_\mu(W_-)^\mu + \frac{1}{8}v^2(g^2+g_w^2)Z_\mu^2+\frac{1}{8}v^2\cdot 0 \cdot A_\mu^2\)
missä \(A_\mu\):n edessä kerroin \(0\). Tämä tarkoittaa sitä, että Higgsin kentän ja fotonikentän välistä vuorovaikutusta ei ole. Kertoimet termien edessä tulkitaan massoiksi
\(\begin{align*}
m_W^2 &=\frac{1}{4}v^2 g_w^2\\
m_Z^2&=\frac{1}{4}v^2(g^2+g_w^2)\\
m_A &= 0
\end{align*}\)
Spontaanissa \(U(1) \times SU(2)\)-symmetriarikossa fotoni pysyy massattomana, mutta Higgsin kenttä antaa massan vektoribosoneille \(W^+\), \(W^-\) ja \(Z\).
Toivottavasti mun kirjoitukset ei ole spämmiä, kun en toisessakaan viestissä päässyt siihen asti, että Diracin kentällä on massa. Tulee kolmas myöhemmin
Tästä voisin jatkaa. Lokaalit \(U(1)\)- ja \(SU(2)\)-symmetriat toteuttava Lagrangen tiheys oliQS kirjoitti: \begin{align*}
V(\Phi)&=-\rho^2\Phi^\dagger\Phi+\lambda(\Phi^\dagger\Phi)^2 \\
&=-\rho^2\phi_1^\dagger\phi_1+\lambda(\phi_1^\dagger\phi_1)^2-\rho^2\phi_2^\dagger\phi_2+\lambda(\phi_2^\dagger\phi_2)^2 \\
&=V(\phi_1)+V(\phi_2)
\end{align*}
\(\begin{align*}
\mathcal{L}_{EM+B+H}&=((\partial_\mu+ig_wB_\mu+igA_\mu)\Phi^\dagger)((\partial^\mu-ig_wB^\mu-igA^\mu)\Phi)+\rho^2\Phi^\dagger\Phi-\lambda(\Phi^\dagger\Phi)^2 \\
&=((\partial_\mu+ig_w[\ (W_\mu)_i\frac{\sigma_i}{2} \ ]+igA_\mu)\Phi^\dagger)((\partial^\mu-ig_w[\ (W^\mu)_i\frac{\sigma_i}{2} \ ]-igA^\mu)\Phi)-V(\Phi^\dagger\Phi)
\end{align*}\)
missä yhdistetty mittakentät \(A^\mu\) ja \(B^\mu\) sekä kompleksinen skalaarikenttä \(\Phi\) (Higgsin dupletti). Toisella rivillä potentiaali \(V(\Phi^\dagger\Phi)\), ja \(SU(2)\)-mittakenttä komponenteilla \(W_1\), \(W_2\) ja \(W_3\).
Kuvassa pystyakseli on \(V\) ja vaaka-akseli \(\Phi\).

Vasemmalla \(V\) minimoituu, kun \(\Phi=0\), ja parametrit \(\rho=0\), \(\lambda>0\).
Keskellä \(\rho>0\) ja \(\lambda>0\). Minimi on kahdessa eri paikassa.
Higgsin potenatiaali on likimain kuten oikeanpuoleinen kuva. Minimi \(V=0\) on kahdessa eri paikassa, joissa kentän arvo \(\Phi \neq 0\).
Minimi saavutetaan siis kohdissa, joissa kentän arvo on nollasta poikkeava. Vaaka-akselin pitäisi tosin olla taso \((\ Re(\Phi), Im(\Phi)\ )\), missä \(V(\Phi)=0\) muodostaa kuuluisan meksikolaisen hatun alimman kohdan. Potentiaalin minimoi kenttä, jolle kaikissa avaruuden pisteissä \(x\) pätee \(\Phi^\dagger\Phi=\frac{\rho^2}{2\lambda}\).
Usein sanotaan, että \(U(1) \times SU(2)\)-symmetria rikkoutuu spontaanisti, kun \(V(\Phi)\):n konfiguraatio siirtyy vasemman kuvan tilanteesta kohti oikeaa. Ennen symmetriarikkoa Diracin kenttä on massaton ja sen Lagrange lokaalisti \(SU(2)\)-symmetrinen.
Skalaari-dupletin \(\Phi\) komponenteilla \(\phi_1\) ja \(\phi_2\) on potentiaalit \(V(\phi_1^\dagger\phi_1)\) ja \(V(\phi_2^\dagger\phi_2)\) sekä näiden minimit. Minimejä vastaavat arvot ovat \(\phi_{1min}\) ja \(\phi_{2min}\). On ääretön määrä minimin tuottavia kentän arvoja, jotka ovat origoa kiertävällä ympyrällä. Arvoista poimitaan mittavalinta. Hyväksi valinnaksi osoittautuu (perustelut sikseen)
\(\Phi_{min}=\begin{pmatrix} \phi_{1min}\\\phi_{2min} \end{pmatrix} = \frac{1}{\sqrt{2}}\begin{pmatrix} 0\\ v+\eta \end{pmatrix}\)
missä \(v = \pm \sqrt{\frac{\rho^2}{\lambda}}\) on vakio, ja \(\eta\) on kenttä, joka korvaa komponentit \(\phi_1\) ja \(\phi_2\). Valinnan nimitys on unitaarimitta. Dupletin \(\Phi\) neljästä arvosta (2 reaalista, 2 kompleksista) jäljellä on yksi reaalinen \(\eta\), jonka nimi on Higgsin kenttä. Loput 3 ovat poistuneet mittavalinnan seurauksena, ja lisäksi \(V(\Phi^\dagger\Phi)\) minimoituu Higgsin kentän arvolla \(\eta=0\).
Lagrangen tiheyteen \(\mathcal{L}_{EM+B+H}\) sijoitetaan Higgsin potentiaalin minimiä \(V(\Phi^\dagger\Phi)=0\) vastaava Higgsin dupletti \(\Phi_{min}\) siten, että käytetään unitaarimittaa
\(\mathcal{L}_{EM+B+H}^{\text{unitary}} = \frac{v^2}{8}\left[g_w^2 (W_1^\mu)^2+g_w^2 (W_2^\mu)^2+ (g_w W^\mu_3-gA^\mu)^2\right]\)
Määritellään \(SU(2)\)-mittakenttä hiukan toisin
\(\begin{align*}
W_+^\mu&=\frac{1}{\sqrt{2}}(W_1^\mu-iW_2^\mu)\\
W_-^\mu&=\frac{1}{\sqrt{2}}(W_1^\mu+iW_2^\mu)
\end{align*}\)
jolloin
\(\mathcal{L}_{EM+B+H}^{\text{unitary}} = \frac{1}{4}v^2 g_w^2 (W_+)_\mu(W_-)^\mu + \frac{1}{8}v^2(g_w W^\mu_3-gA^\mu)^2\)
Jälkimmäinen termi voidaan kirjoittaa matriisimuodossa
\((g_w W^\mu_3-gA^\mu)^2 = (W_3^\mu,A_\mu)
\begin{bmatrix}
g_w^2 & -gg_w \\
-gg_w & g^2
\end{bmatrix}
\begin{pmatrix} W_3^\mu \\ A_\mu \end{pmatrix}\)
missä matriisin molemmin puolin vektori \((W_3^\mu,A_\mu)\). Matriisi diagonalisoidaan, ja \(W_3^\mu\) nimetään erinäisiä kertoimia käyttäen \(Z^\mu\) (perustelu jääköön sikseen tässä kohti). Näin saadaan
\(\mathcal{L}_{EM+B+H}^{\text{unitary}} = \frac{1}{4}v^2 g_w^2 (W_+)_\mu(W_-)^\mu + \frac{1}{8}v^2(g^2+g_w^2)Z_\mu^2+\frac{1}{8}v^2\cdot 0 \cdot A_\mu^2\)
missä \(A_\mu\):n edessä kerroin \(0\). Tämä tarkoittaa sitä, että Higgsin kentän ja fotonikentän välistä vuorovaikutusta ei ole. Kertoimet termien edessä tulkitaan massoiksi
\(\begin{align*}
m_W^2 &=\frac{1}{4}v^2 g_w^2\\
m_Z^2&=\frac{1}{4}v^2(g^2+g_w^2)\\
m_A &= 0
\end{align*}\)
Spontaanissa \(U(1) \times SU(2)\)-symmetriarikossa fotoni pysyy massattomana, mutta Higgsin kenttä antaa massan vektoribosoneille \(W^+\), \(W^-\) ja \(Z\).
Toivottavasti mun kirjoitukset ei ole spämmiä, kun en toisessakaan viestissä päässyt siihen asti, että Diracin kentällä on massa. Tulee kolmas myöhemmin
Mikä estäisi tulkitsemasta niin, että potentiaali on minimissä samankertaisesti vakiolla positiivisella ja negatiivisella resonaattorilla, jolloin kentän odotusarvo olisi kuitenkin keskimäärin nolla ja mekanismin rakenne symmetrinen? Symmetria rikkoutuisi vastakkaisille eli antipodaalisille aine-/antiaine-vaiheille erikseen...
Nykyisessä matemaattisessa kuvauksessa tarvitaan singlettejä erottelemaan oikeakätiset hiukkaset, mutta eikö vuorovaiheisuus mahdollistaisi molemmille sektoreille oman spontaanin symmetriarikon dupletteineen ja Higgsin kentän arvo molemmat sektorit huomioiden olisi keskimäärin nolla - symmetria täydellistyisi.
Tästä saisi perusteen sähkövarauksille ajanluonteisissa hiukkasissa ja magneettivarauksille avaruudenluonteisissa poikkileikkauksissa...
Nykyisessä matemaattisessa kuvauksessa tarvitaan singlettejä erottelemaan oikeakätiset hiukkaset, mutta eikö vuorovaiheisuus mahdollistaisi molemmille sektoreille oman spontaanin symmetriarikon dupletteineen ja Higgsin kentän arvo molemmat sektorit huomioiden olisi keskimäärin nolla - symmetria täydellistyisi.
Tästä saisi perusteen sähkövarauksille ajanluonteisissa hiukkasissa ja magneettivarauksille avaruudenluonteisissa poikkileikkauksissa...
Hienorakennevakio vapausasteista: (1⁰+2¹+3²+5³+1/2¹*3²/5³)⁻¹ = 137,036⁻¹
Higgsin kentän vakuumiodotusarvo on kokeellisestikin todettu olevan n. 246 GeV, joten nolla se ei mitä ilmeisimmin ole.
Oikeakiraalisen kentän singletti tarvitaan, kyllä. Syy on se, että heikko vuorovaikutus ei saa miksata oikeakiraalisia hiukkasia, vaan ne muuntuvat SU(2)-ryhmän triviaalina esityksenä, mikä tarkoittaa karkeasti ottaen 1:llä kertomista (ei muunnosta).
Vasenkiraaliset kentät ovat dupletteja, joiden komponentit miksautuvat heikossa vuorovaikutuksessa.
Oikeakiraalisen kentän singletti tarvitaan, kyllä. Syy on se, että heikko vuorovaikutus ei saa miksata oikeakiraalisia hiukkasia, vaan ne muuntuvat SU(2)-ryhmän triviaalina esityksenä, mikä tarkoittaa karkeasti ottaen 1:llä kertomista (ei muunnosta).
Vasenkiraaliset kentät ovat dupletteja, joiden komponentit miksautuvat heikossa vuorovaikutuksessa.
Esittämässäni asetelmassa mittaus tapahtuu aina jommassa kummassa antipodaalisektorissa, jonka suhteen saadaan tietysti tuo energia. Mutta Higgsin mekaniikan matematiikassa efektiivistä on \(H^2\) eli \(H\) sinänsä voisi olla negatiivinenkin tulosten muuttumatta.
Eräs näkymä on sellainen, jossa meillä on lomittuneet peilikuvakaikkeudet noina kahtena sektorina ja erillisyysjatkumon diversiot osoittavat vaihesektoreissa vastakkaisiin suuntiin - kansankielellä: eräälle koordinaatistolle projisoituu vastakkaisvaiheen sektorin ajan suunta vastakkaisena oman koordinaatiston aikakehitykseen nähden ja siksi rakenne saa vastakkaisen varauksen.
Tämän mallin kanssa yhteensopivaa on, etteivät vastakkaiset varaukset vuorovaikuta keskenään sähköisesti; ne putoavat kentän summavaikutuksena vastaavalla voimakkuudella toisiinsa kuin samanmerkkisten varausten voi puolestaan katsoa vuorovaikuttavan sähköisesti hylkien (pitävän erillisyyttä) keskenään.
Eli tyhjön odotusarvo \(H\) voi periaatteessa aivan hyvin olla n. \(246 \: GeV/c²\) tai \(-246 \: GeV/c²\) sektoreittain mittaustulosten puitteissa.
Onko jotain muuta, joka torjuisi tulkinnan antipodaaleista vaihesektoreista? Olisiko jokin koejärjestely, jolla vaikka epäsuorastikin voitaisiin asiaa testata?
Vai voisiko olla niin, että toive löytää aineen ja antiaineen määräeroa selittävä symmetriarikko onkin ohjannut fysiikan matematiikan valintoja?
Eräs näkymä on sellainen, jossa meillä on lomittuneet peilikuvakaikkeudet noina kahtena sektorina ja erillisyysjatkumon diversiot osoittavat vaihesektoreissa vastakkaisiin suuntiin - kansankielellä: eräälle koordinaatistolle projisoituu vastakkaisvaiheen sektorin ajan suunta vastakkaisena oman koordinaatiston aikakehitykseen nähden ja siksi rakenne saa vastakkaisen varauksen.
Tämän mallin kanssa yhteensopivaa on, etteivät vastakkaiset varaukset vuorovaikuta keskenään sähköisesti; ne putoavat kentän summavaikutuksena vastaavalla voimakkuudella toisiinsa kuin samanmerkkisten varausten voi puolestaan katsoa vuorovaikuttavan sähköisesti hylkien (pitävän erillisyyttä) keskenään.
Eli tyhjön odotusarvo \(H\) voi periaatteessa aivan hyvin olla n. \(246 \: GeV/c²\) tai \(-246 \: GeV/c²\) sektoreittain mittaustulosten puitteissa.
Onko jotain muuta, joka torjuisi tulkinnan antipodaaleista vaihesektoreista? Olisiko jokin koejärjestely, jolla vaikka epäsuorastikin voitaisiin asiaa testata?
Vai voisiko olla niin, että toive löytää aineen ja antiaineen määräeroa selittävä symmetriarikko onkin ohjannut fysiikan matematiikan valintoja?
Hienorakennevakio vapausasteista: (1⁰+2¹+3²+5³+1/2¹*3²/5³)⁻¹ = 137,036⁻¹
Yksiköistä sen verran, että odotusarvon yksikkö on GeV. Higgsin bosonin massa on n. 125 \(GeV/c^2\).Eusa kirjoitti: ↑22.9.2024, 12:52 Esittämässäni asetelmassa mittaus tapahtuu aina jommassa kummassa antipodaalisektorissa, jonka suhteen saadaan tietysti tuo energia. Mutta Higgsin mekaniikan matematiikassa efektiivistä on \(H^2\) eli \(H\) sinänsä voisi olla negatiivinenkin tulosten
...
tyhjön odotusarvo \(H\) voi periaatteessa aivan hyvin olla n. \(246 \: GeV/c²\) tai \(-246 \: GeV/c²\) sektoreittain mittaustulosten puitteissa.
Odotusarvo ei riipu kentän 'paikasta sombreron kuoppassa' (edellisten kuvien kuula). Potentiaalin minimoi kenttä, jolle pätee \(\Phi^\dagger\Phi=\frac{\rho^2}{2\lambda}\).

\(\Phi\) ja \(\Phi^\dagger\) ovat kompleksilukuja. Nämä voi konkreettisesti kirjoittaa \(\Phi = ve^{i\theta}\) ja \(\Phi^\dagger = ve^{-i\theta}\), missä \(v,\theta \in \mathbb{R}\). Tuo \(v\) on potentiaalin minimi säteen suunnassa, ja \(\theta\) on napakulma.
Potentiaali minimoituu, kun \((ve^{i\theta})^\dagger ve^{i\theta} = \frac{\rho^2}{2\lambda}\), mistä seuraa \(v^2 = \frac{\rho^2}{2\lambda}\). Tämä ei ole kulmasta \(\theta\) riippuva. Higgsin dupletin vakuumiodotusarvo (unitaarimitassa) on
\(\bra{\Phi}0\ket{\Phi} = \frac{1}{\sqrt{2}}\begin{pmatrix} 0\\ v \end{pmatrix}\)
missä kokeellisesti mitattu reaaliluku \(v\) = 246 GeV, jolle ehto \(v^2 = \frac{\rho^2}{2\lambda}\). Periaatteessa siis \(v = \pm \sqrt{\frac{\rho^2}{\lambda}} = \pm 246 GeV\). Etumerkkivalinta ei haittaa, kun Higgsin kenttä antaa massan W ja Z-bosoneille, sillä massat ovat neliöitä
\(
\begin{align*}
m_W^2 &=\frac{1}{4}v^2 g_w^2\\
m_Z^2&=\frac{1}{4}v^2(g^2+g_w^2)\\
\end{align*}\)
Kuitenkin Diracin kentän massa on muotoa
\(m \sim \frac{1}{\sqrt{2}}v\)
missä etumerkki tekisi massasta negatiivisen. Tämän saisi järjestykseen Lagrangen tiheyden etumerkeillä tai vaihtamalla Diracin dupletin komponentit jotenkin keskenään, mutta kätevämpää on kai valita \(v = +246 GeV\).
Higgsin mekanismin spontaanissa symmetriarikossa kenttä 'putoaa' johonkin kohtaan \(\theta\), ja ei sen jälkeen liikku \(\theta\)-suunnassa. Goldstonen bosoni puolestaan kiertää potentiaalikuopassa. Ero näiden välillä on oma juttunsa. Joskus sanotaan, että Goldstonen bosoni poistuu SU(2)-mittabosonin takia ja tilalle tulee Higgs massoineen. Mutta en tiedä miten hyvin tuo asiaa kuvailee.
Jos taas 'sombrero' olisi kallellaan, eli löytyisi yksikäsitteinen minimikohta, niin symmetriarikko ei olisi spontaani, vaan vain symmetriarikko.
Kentän arvoon \(v\) voisi vielä todeta sen, että jos \(\Phi\) ajatellaan täsmällisesti kompleksilukuna, niin \(v\) on kompleksiluvun \(\Phi=a + bi\) itseisarvo, joka määritellään \(|v| = \sqrt{a^2+b^2}\). Tämä on aina positiivinen reaaliluku, joten etumerkkivalinta + on ainoa vaihtoehto. Sehän on paikkavektorin pituus eli etäisyys origosta.