Toimisiko code-taulukot?
...
Palautteita odotellessa pieni päivitys keskittyen erityisesti ketjun aiheeseen eli sähkömagneettisen aallon olemukseen fysikaalisessa ympäristössä.
Completing Relativity — A Topological Spinor Framework for Emergent Electromagnetism
(A global-spinor approach; the field may equally be formulated in ordinary spinor bundles or, as discussed, in a generalised twistor – “wistor” – setting.)
---
Abstract
We develop a differential-geometric extension of general relativity in which quantum behaviour and electromagnetism emerge from a single global \(U(1)\) phase field on the \(\text{Spin}(3,1)\) principal bundle.
Local particles do
not carry intrinsic spinors; rather, the global phase \(\Phi\) projects rhythmic structures into space-time.
The spatial gradient of that phase defines a
mass-density field \(\rho(x)=\lVert\nabla\!\arg\Phi\rVert\); gravity is then experienced as free fall along \(-\nabla\ln\rho\).
Electromagnetism is the curvature of the \(U(1)\) connection \(A=\Phi^{-1}d\Phi\).
While our rigid derivations rely only on four-dimensional geometry, Section 7 shows how the same structures appear naturally inside a generalised twistor (wistor) framework that incorporates a Klein-bottle phase surface.
---
1 Introduction
Two pillars of modern physics remain conceptually disjoint: general relativity (GR) describes causal geometry; quantum field theory (QFT) relies on local operator algebras.
We eliminate the gap by positing that
all dynamical content is encoded in a
global \(U(1)\) phase
\(\Phi : P \;\to\; U(1), \qquad P \xrightarrow{\text{Spin}(3,1)} M,\)
with no local spinorial degrees of freedom attached to matter.
The global phase may be realised either
(i) as a conventional spinor field on \(P\) or
(ii) in a generalised twistor (“wistor”) picture where space-time points correspond to \(\text{CP}^{1}\) fibres on a Klein-bottle sheet — reserved for the Discussion.
Postulate I – Global Phase Every space-time point possesses a unique, \(\text{Spin}(3,1)\)-equivariant \(U(1)\) phase.
Postulate II – Neutral-Fibre Coupling Positive and negative electric sectors are disjoint sections of the same \(U(1)\) bundle, interacting only through neutral fibres that conserve energy.
Postulate III – Entropic Proper Time Time equals the statistical loop-rate of entropic evolution; proper time is the geodesic average of that rate.
Readers preferring twistor geometry may jump ahead to Section 7.
---
2 Mathematical Foundation
2.1 Spin Bundle and Mass Density
Let \((M,g)\) be a four-dimensional pseudo-Riemannian manifold (signature \(-+++\)).
Define a global phase \(\Phi\) on the \(\text{Spin}(3,1)\) principal bundle; the \(U(1)\) connection and curvature read
\(A:=\Phi^{-1}d\Phi, \qquad F=dA.\)
We
identify Maxwell’s tensor with \(F\).
The
mass-density field is
\(\rho(x):=\lVert\nabla\!\arg\Phi(x)\rVert, \qquad a^{\mu}=-\nabla^{\mu}\ln\rho.\)
Constant \(\rho\) reproduces inertial frames; gradients yield the observed gravitational acceleration.
2.2 Dirac Dynamics as Phase Transport
Projecting \(\Phi\) into the Clifford bundle gives a local spinor \(\psi\).
The usual Dirac operator \(\mathcal D_{A}\) satisfies
\(\gamma^{\mu}\partial_{\mu}\arg\Phi \;=\; \rho(x),\)
so mass is not a fixed parameter but the local magnitude of the phase gradient.
---
3 Maxwell Equations as Topological Identities
Because \(F=dA\), the Bianchi identity \(dF=0\) and current conservation \(\nabla^{\mu}F_{\mu\nu}=J_{\nu}\) follow directly.
Charge is a topological degeneracy of \(\Phi\).
---
4 Relativistic Dynamics without Superposition
During each Planck-time phase loop only one projection of \(\Phi\) is realised; alternative branches remain virtual, eliminating ontic superposition.
Entanglement occurs when two points share the same global phase modulo \(2\pi\).
---
5 Rigid Results
Koodi: Valitse kaikki
' Phenomenon ' Standard description ' Present framework
' --------------------------------------------------------------------------------------------
' Electromagnetism ' Local U(1) gauge field A_mu ' Curvature of A = Φ^{-1} dΦ
' Mass term ' Constant m ' Local phase-gradient norm ρ(x)
' Gravity ' Metric curvature R_{μν} ' Free fall along −∇ ln ρ
' Superposition ' Linear state combination ' Non-realised phase branches
' Entanglement ' Non-local wavefunction ' Equal global phase at distinct points
---
6 Conclusions
A single global \(U(1)\) phase field recreates the empirical content of GR and QED: Maxwell’s equations arise from curvature, Dirac dynamics from phase transport, and gravity from the gradient of mass density.
The framework is self-contained in four dimensions; a twistor (wistor) interpretation provides complementary insights but is not essential.
---
7 Discussion
7.1 Twistor / Wistor Realisation and Klein-Bottle Topology
In twistor theory each point of complexified Minkowski space corresponds to a Riemann sphere (\(\text{CP}^{1}\)) inside twistor space \(\mathbb{CP}^{3}\).
To accommodate the *global phase* philosophy, we enlarge this construction into a
wistor space \(\mathcal W\) where CP\(^1\) fibres are glued to a non-orientable
Klein-bottle sheet:
* The Klein surface identifies antipodal points after a 180° rotation, encoding the sign flip between positive- and negative-charge sectors.
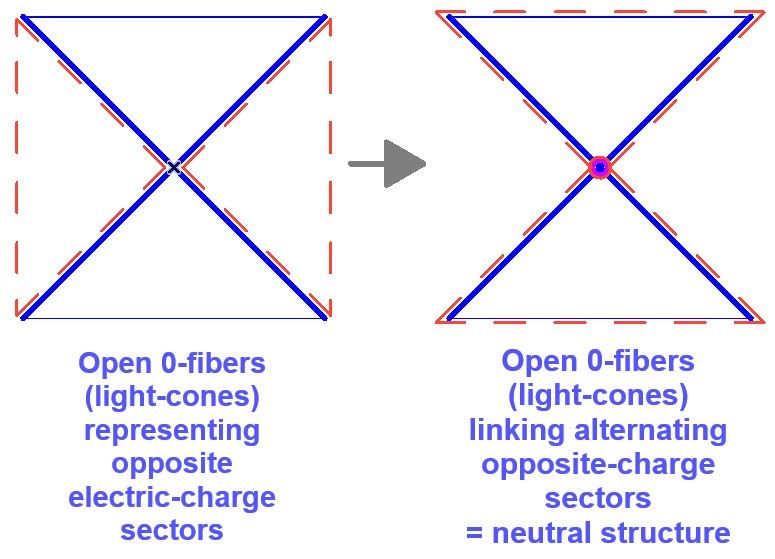
* Open 0-fibres attached to opposite rims represent causal lines of the two sectors; they remain disjoint in the absence of neutral linkages.
* A
neutral linkage occurs when a real space-time loop executes a half-turn relative to the conformal background; the two fibres then meet on the Klein surface, allowing energy-preserving exchange (Figure A1).
Within \(\mathcal W\) the global phase \(\Phi\) becomes a holomorphic section; its curvature matches the \(U(1)\) connection used in Sections 2–3.
The wistor integral formula reproduces classical fields but automatically embeds mass density as the norm of holomorphic phase gradients.
Hence twistor geometry is fully compatible with our four-dimensional derivation while revealing
why electric sectors decouple and re-join only via neutral structures.
7.2 Pilot-Wave Field from Null-Geodesic Carrier Modes
7.2.1 Carrier-lattice picture
Bohm’s
pilot wave is realised as a lattice of standing null-geodesic fibres whose phases are locked to the global pinor \(\Phi\).
Each 0-fibre is a spin-\(\tfrac12\) carrier mode; two antipodal modes combine into a spin-1 **bosonic channel**.
Energy pulses therefore follow pre-existing guidance tracks—no real-time “wavefunction collapse” is required.
7.2.2 Photon, half neutrino and half photon states
Koodi: Valitse kaikki
' θ (angle) ' Physical state ' Description
' ---------------------------------------------------------------
' 0 ' basic 1-form ' electric carrier signal
' π/2 ' half neutrino ' chiral phase signal; no energy transfer
' π ' half photon ' pulsed push among like charges
' ± pair ' bosonic photon ' coherent EM wave
Two 0-fibre phases give
\(I(x)=4\cos^{2}(k\cdot\Delta x/2)\)
— identical to Schrödinger interference.
2. Bell correlations Möbius holonomy \(-1\) yields
\(E(a,b)=-a\cdot b\), so CHSH \(S=2\sqrt{2}\).
3. Macro-decoherence For \(N \gg 1\) random tilts,
\(\langle e^{i(\phi_j-\phi_k)}\rangle \sim e^{-N\sigma^{2}/2}\);
interference vanishes when \(N \ge N_{\text{dec}}\).
Result — Interference, Bell violation, and decoherence all follow from the topological pinor lattice without invoking ontic superposition.
Outlook
* Gravitational waves may be re-interpreted as propagating modulations in \(\rho\) or as oscillatory deformations of the Klein surface.
* Particle taxonomy could arise from topologically stable \(\text{CP}^{1}\) fibrations linked by neutral loops, generalising skyrmion models.
* Experimental signature: phase-gradient correlations might imprint distinctive polarisation patterns in cosmic backgrounds.
---
References
[1] S. Kobayashi & K. Nomizu,
Foundations of Differential Geometry, Vols I–II (Wiley, 1963).
[2] R. Penrose & W. Rindler,
Spinors and Space-Time, Vol. II (CUP, 1986).
[3] M. Nakahara,
Geometry, Topology and Physics, 2nd ed. (Taylor & Francis, 2003).
[4] N. M. J. Woodhouse,
Geometric Quantization (OUP, 1997).
[5] C. J. Isham,
Modern Differential Geometry for Physicists (World Scientific, 1999).
[6] D. Dürr, S. Goldstein & N. Zanghì, “Quantum Equilibrium and the Origin of Absolute Uncertainty”,
J. Stat. Phys. 67, 843 (1992).
[7] D. Dürr & S. Teufel,
Bohmian Mechanics (Springer, 2009).
---
Appendix A – Neutral-Linkage Diagram
- Electric-sectors.jpg (57.29 KiB) Katsottu 542 kertaa
Figure A1. Opposite-charge null fibres (left), tachyonic to each other, and their neutral linkage produced by a 180° null-fibre loop phase (right).