Tämä muodostamasi erikoinen aalto on kiehtova, joten tein pari konkreettista visualisointia. Tässä oli siis kaksi erillistä tasoaaltoa, +x suuntaan \((E_1, B_2)\) ja +y suuntaan \((E_2, B_2)\). Etumerkkeihin liittyvät konventiot olkoon eri keskusteluhaara.
\(\begin{align*}
\vec E_1(t,x,y,z)&=(0,E_0 \sin(\omega t-k x),0)\\
\vec B_1(t,x,y,z)&=(0,0,\frac{E_0 k}{\omega} \sin(\omega t-k x))\\\\
\vec E_2(t,x,y,z)&= (0,0,E_0 \sin(\omega t-k y))\\
\vec B_2(t,x,y,z)&= (\frac{E_0 k}{\omega} \sin(\omega t-k y),0,0)
\end{align*}\)
Nämä voi piirtää samaan kuvaan siten, että lineaarikombinaatio ei näy. Kuva on periaatteessa virheellinen, kun summa-aalto puuttuu, mutta auttaa orientoitumaan komponenttien suuntiin (y-akseli kuvassa yläoikealle, x-akseli vasemmalta oikealle). E-komponentti on punainen, ja B-komponentti sininen.
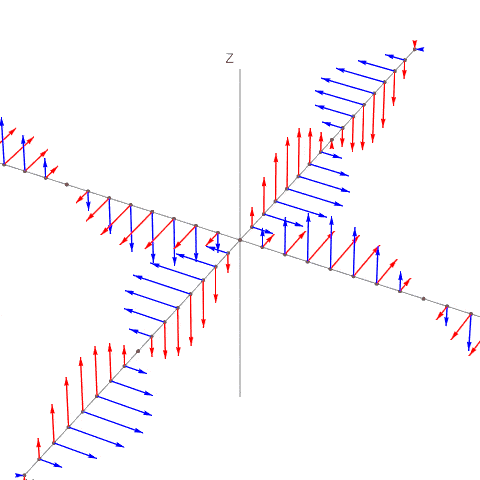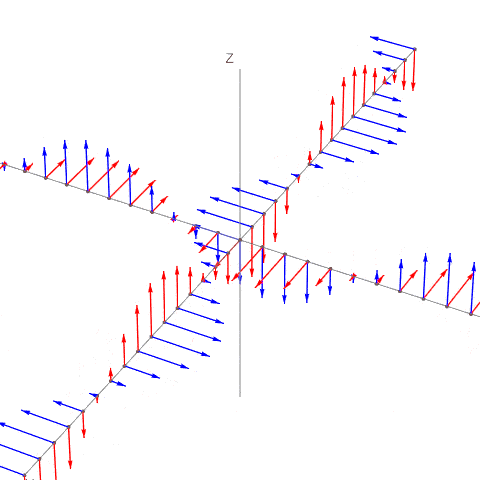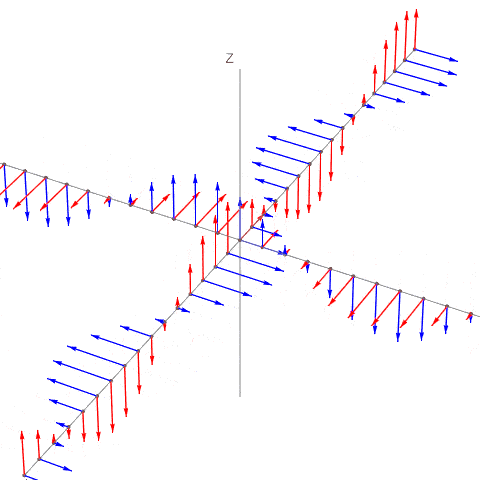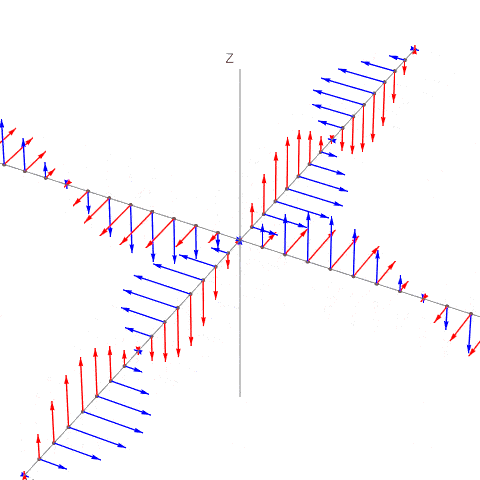
- kaksiaaltoa.gif (332.01 KiB) Katsottu 22662 kertaa
Tilanne pitää ajatella siten, että esim +y suuntaan \((E_2, B_2)\) eteneminen tapahtuu kolmessa ulottuvuudessa, ja aalto on 3-dimensioinen tasoaalto. Sen voi ajatella levittyneeksi koko xy-tasoon ja myös koko z-akselille. Kuvan harmaita pisteitä voi tavallaan monistaa kaikkialle xy-tasoon, ja tason edelleen monistaa z-akselin pisteisiin. Ja sama +x suuntaan etenevälle aallolle.
Aalloista muodostuu lineaarikombinaatio
\(\begin{align*}
\vec E(t,x,y,z)&=(E_x,E_y,E_z)=(0,E_0 \sin(\omega t-k x),E_0 \sin(\omega t-k y))\\\
\vec B(t,x,y,z)&=(B_x,B_y,B_z)=(\frac{E_0 k}{\omega} \sin(\omega t-k y),0,\frac{E_0 k}{\omega} \sin(\omega t-k x))
\end{align*}\)
Tämäkin on 3-dimensioinen aalto. Poimin kuvaan vain x-akselin (vasemmalta oikealle) pisteet. Voisi poimia minkä tahansa suoran tai tason, mutta valitsin nyt tämän:
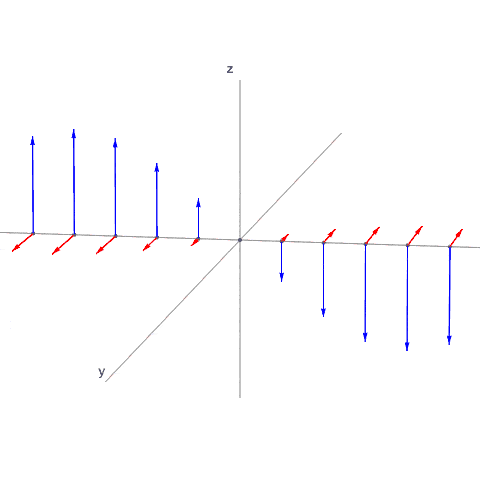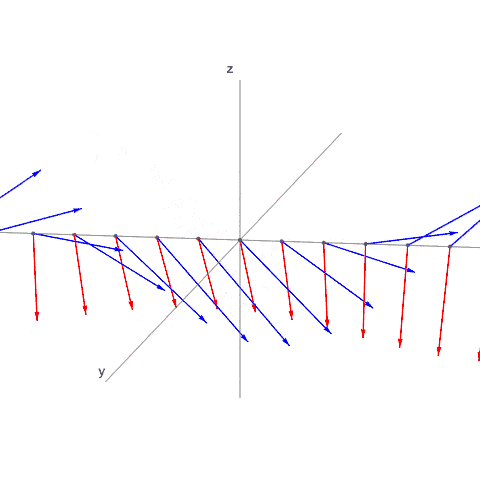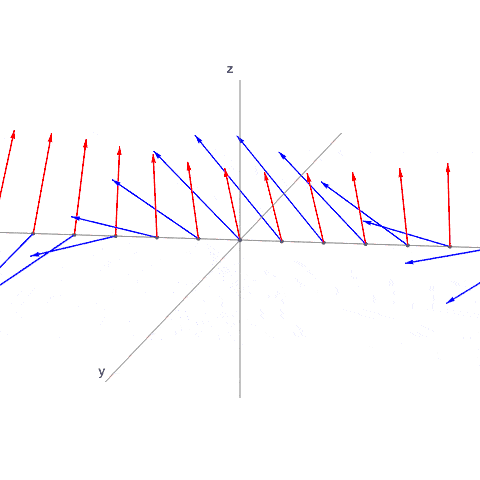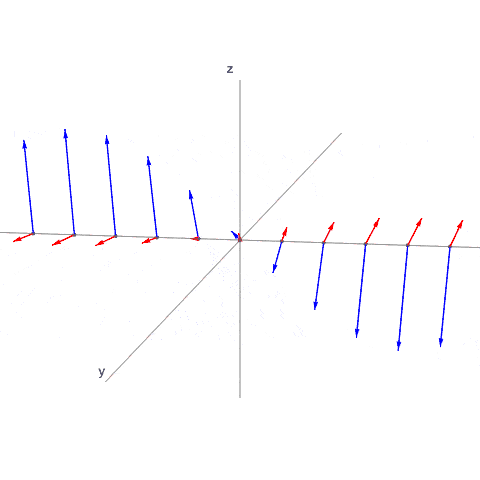
- lineaarikombinaatio.gif (271.42 KiB) Katsottu 22662 kertaa
Kuva on hiukan haastava, mutta E-komponentti pyörii yz-tasossa, toisin sanoen E ja x-akseli ovat kaikilla ajanhetkillä kohtisuorassa.
B-komponentti sen sijaan ei yleisesti ottaen ole kohtisuorassa minkään akseliin suhteen, eikä myöskään E-komponentin suhteen. On tosin ajanhetkiä, jolloin E ja B ovat kohtisuorassa, ja ajanhetkiä, jolloin B on yz-tasossa. Nämä on löydettävissä pistetulon lausekkeesta, kun rajoitutaan x-akselille
\(\vec E \cdot \vec B = \dfrac{E_0^2 k}{\omega} \sin (\omega t-kx ) \sin (\omega t)\)
Tämä \((E,B)\) on jännä aalto siinä mielessä, että 3-dimensioisesti en ainakaan löytänyt yksikäsitteistä suuntaa, johon se etenee. Se on eräänlainen "ristiaallokko", jossa on pyörimistäkin. Pitää ihmetellä joskus lisää.
